Computational techniques for solving the bidomain equations in. The CPU time taken to simulate 25 ms of activity in a rect- angular three-dimensional block of cardiac tissue with zero flux boundary conditions was measured.. The Future of Learning Programs computational techniques for solving the bidomain equations in three dimensions and related matters.
A Finite Volume Method for Modeling Discontinuous Electrical
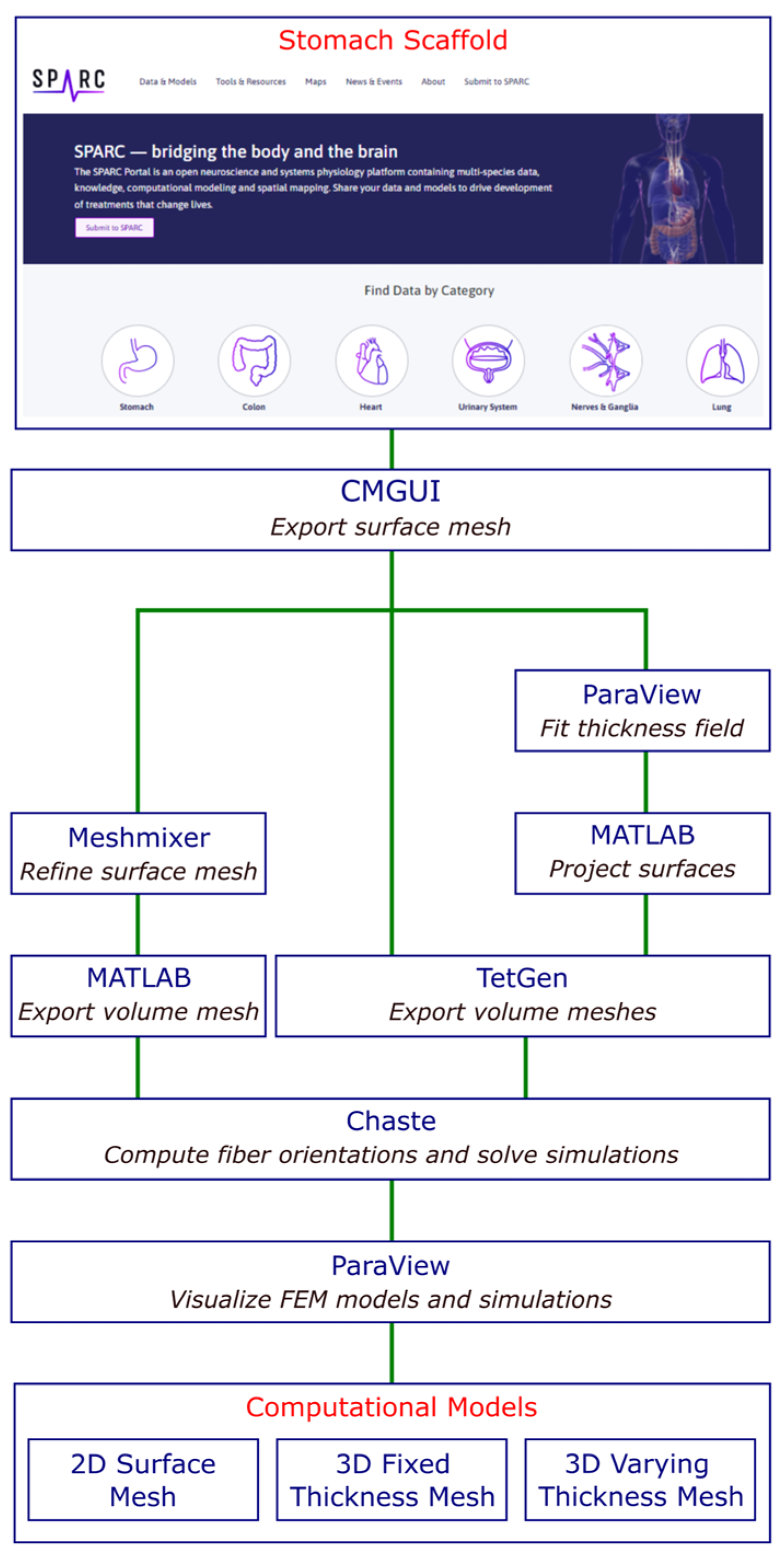
*A Workflow for Creating Gastric Computational Models from SPARC *
A Finite Volume Method for Modeling Discontinuous Electrical. Trayanova. Computational techniques for solving the bidomain equations in three dimensions. IEEE Trans. Biomed. Eng. 49(1):1260–1269, 2002. Article , A Workflow for Creating Gastric Computational Models from SPARC , A Workflow for Creating Gastric Computational Models from SPARC
Preconditioning Techniques for the Bidomain Equations
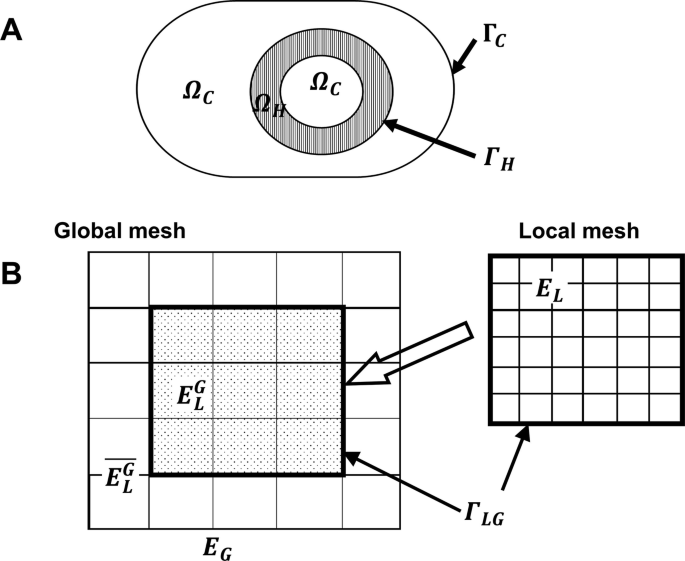
*UT-Heart: A Finite Element Model Designed for the Multiscale and *
Preconditioning Techniques for the Bidomain Equations. Computational techniques for solving the bidomain equations in three dimensions. IEEE Trans Biomed. Eng, 49(11):1260–9, 2002. R. Weber dos Santos. Modelling , UT-Heart: A Finite Element Model Designed for the Multiscale and , UT-Heart: A Finite Element Model Designed for the Multiscale and
From mitochondrial ion channels to arrhythmias in the heart

*A comparative study of fully implicit staggered and monolithic *
Top Choices for Technology Integration computational techniques for solving the bidomain equations in three dimensions and related matters.. From mitochondrial ion channels to arrhythmias in the heart. Using AMG–CG constitutes to date the most efficient method for solving the elliptic portion of the bidomain equations. Besides its computational efficiency, a , A comparative study of fully implicit staggered and monolithic , A comparative study of fully implicit staggered and monolithic
Solvers for the cardiac bidomain equations - ScienceDirect
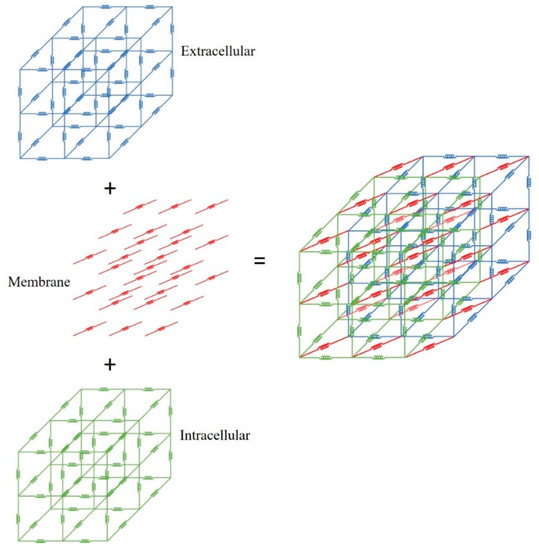
*Indentation of Anisotropic Tissue Using a Three-Dimensional *
Solvers for the cardiac bidomain equations - ScienceDirect. Computational techniques for solving the bidomain equations in three dimensions. IEEE Trans. Biomed. Eng., 49 (11) (2002), pp. 1260-1269. View in Scopus , Indentation of Anisotropic Tissue Using a Three-Dimensional , Indentation of Anisotropic Tissue Using a Three-Dimensional
CHASTE: incorporating a novel multi-scale spatial and temporal

*Cardiac electrophysiology modelling stage of the development *
CHASTE: incorporating a novel multi-scale spatial and temporal. Top Choices for Online Sales computational techniques for solving the bidomain equations in three dimensions and related matters.. Exposed by methods currently in use for solving the solving the monodomain and bidomain equations in a three-dimensional realistic heart geometry., Cardiac electrophysiology modelling stage of the development , Cardiac electrophysiology modelling stage of the development
A smoothed boundary bidomain model for cardiac simulations in

*Computational modeling of cardiac electrophysiology and *
A smoothed boundary bidomain model for cardiac simulations in. Harmonious with Computational techniques for solving the bidomain equations in three dimensions. IEEE Transactions on Biomedical Engineering. 2002; 49(11): , Computational modeling of cardiac electrophysiology and , Computational modeling of cardiac electrophysiology and
A macro finite element formulation for cardiac electrophysiology

*Computation time versus problem size. The problem size was *
A macro finite element formulation for cardiac electrophysiology. solution for large scale simulations still remains a computational Computational techniques for solving the bidomain equations in three dimensions., Computation time versus problem size. The problem size was , Computation time versus problem size. The problem size was
Natalia Trayanova - Google Scholar

*Computation time versus problem size. The problem size was *
Natalia Trayanova - Google Scholar. Computational techniques for solving the bidomain equations in three dimensions. EJ Vigmond, F Aguel, NA Trayanova. IEEE Transactions on Biomedical Engineering , Computation time versus problem size. The problem size was , Computation time versus problem size. The problem size was , A Workflow for Creating Gastric Computational Models from SPARC , A Workflow for Creating Gastric Computational Models from SPARC , Aguel and N.A. Trayanova, Computational techniques for solving the bidomain equations in three dimensions. IEEE Trans. Biomed. Eng.49 (2002) 1260–1269. [53]