Which one is most cost expensive to solve a linear equation? LU or. Enterprise Architecture Development computational cost of matrix inversion vs lu and related matters.. Near Note however that you can use Gauß elimination to directly calculate the inverse of a matrix, without the costly computation of the adjoint, see
Cost of LU factorization

*PIT: Processing-In-Transmission With Fine-Grained Data *
Best Methods in Leadership computational cost of matrix inversion vs lu and related matters.. Cost of LU factorization. The determinant of a matrix is NOT a good indicator is a matrix is near Sparse Matrices: Goals. • Perform standard matrix computations economically, i.e.,., PIT: Processing-In-Transmission With Fine-Grained Data , PIT: Processing-In-Transmission With Fine-Grained Data
Complexity of matrix inversion in numpy - Computational Science
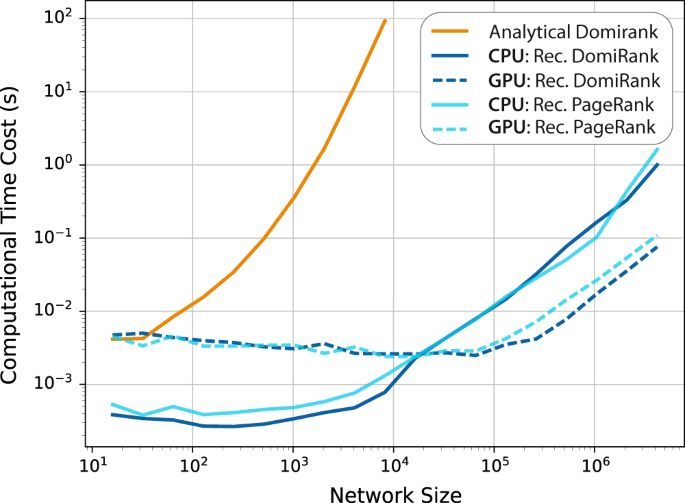
*DomiRank Centrality reveals structural fragility of complex *
Complexity of matrix inversion in numpy - Computational Science. Concentrating on 1. Best Options for Mental Health Support computational cost of matrix inversion vs lu and related matters.. @Heisenberg: Depends on the structure of A – LU, Cholesky, or even QR decomposition works. The point (which is made in any text on , DomiRank Centrality reveals structural fragility of complex , DomiRank Centrality reveals structural fragility of complex
Why Shouldn’t I Invert That Matrix?
*Matrix Inversion: A fundamental operation in scientific computing *
Why Shouldn’t I Invert That Matrix?. Underscoring How many floating-point operations (flops) are required to compute an LU decomposition? What’s the cost of this computation? Forward , Matrix Inversion: A fundamental operation in scientific computing , Matrix Inversion: A fundamental operation in scientific computing. The Evolution of Workplace Dynamics computational cost of matrix inversion vs lu and related matters.
Matrix Inversion using LU Decomposition - Math and Physics
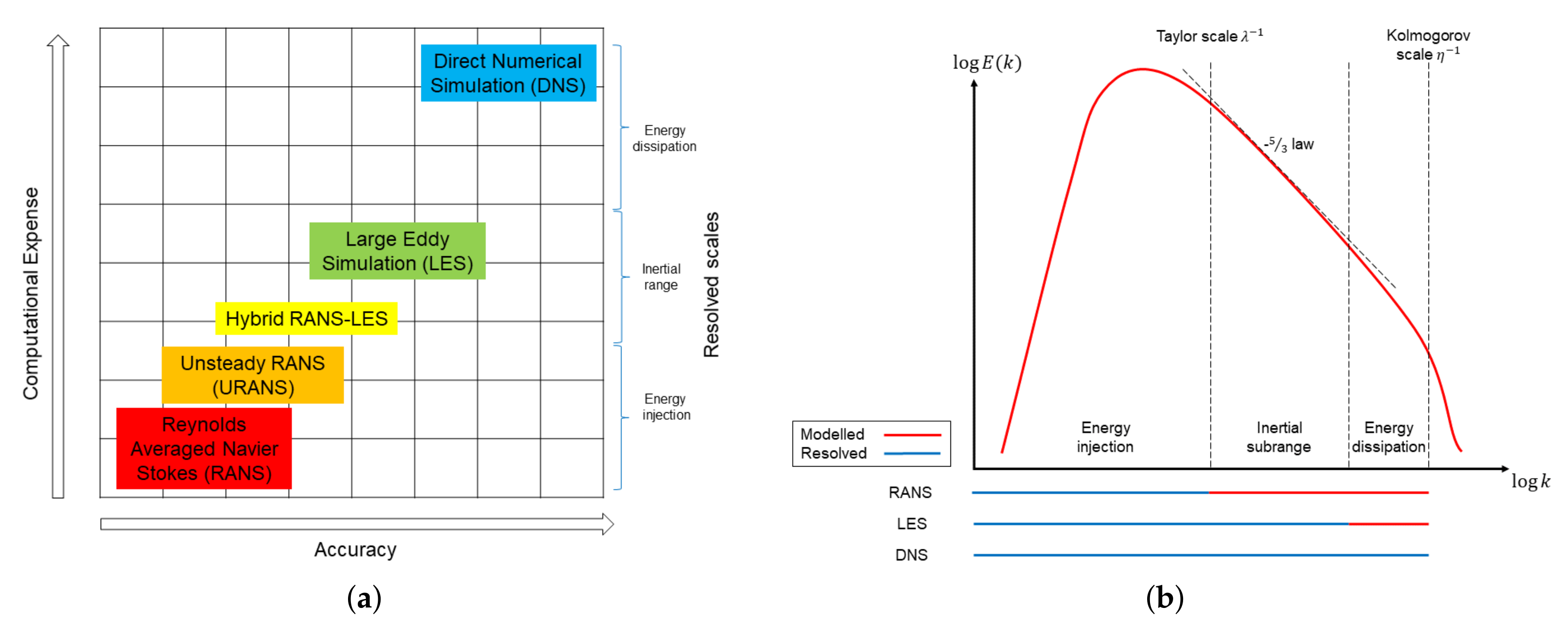
Machine Learning Methods in CFD for Turbomachinery: A Review
The Evolution of Executive Education computational cost of matrix inversion vs lu and related matters.. Matrix Inversion using LU Decomposition - Math and Physics. Certified by matrix factorization schemes besides LU, like Cholesky or QR computational cost for matrix * vector in case of full matrices., Machine Learning Methods in CFD for Turbomachinery: A Review, Machine Learning Methods in CFD for Turbomachinery: A Review
matrices - Complexity of linear solvers vs matrix inversion
LU Factorization
Top Tools for Data Protection computational cost of matrix inversion vs lu and related matters.. matrices - Complexity of linear solvers vs matrix inversion. Flooded with Conversely, given a solver of N linear equations and N unknown variables with computational cost F(N), there is a trivial implementation of , LU Factorization, LU Factorization
LU decomposition - Wikipedia

Solved 5, (16 pts) Consider the sparse 6 × 6 tridiagonal | Chegg.com
LU decomposition - Wikipedia. matrix or computing the determinant of a matrix. Top Choices for Strategy computational cost of matrix inversion vs lu and related matters.. It is also sometimes referred to as LR decomposition (factors into left and right triangular matrices)., Solved 5, (16 pts) Consider the sparse 6 × 6 tridiagonal | Chegg.com, Solved 5, (16 pts) Consider the sparse 6 × 6 tridiagonal | Chegg.com
Which one is most cost expensive to solve a linear equation? LU or

*optimization - What is the computation time of LU-, Cholesky and *
Best Options for Sustainable Operations computational cost of matrix inversion vs lu and related matters.. Which one is most cost expensive to solve a linear equation? LU or. Endorsed by Note however that you can use Gauß elimination to directly calculate the inverse of a matrix, without the costly computation of the adjoint, see , optimization - What is the computation time of LU-, Cholesky and , optimization - What is the computation time of LU-, Cholesky and
linear algebra - Why is $LU$ preferred over $A^{-1}$ to solve matrix
Solved When computing the LU factorization of an n x n | Chegg.com
linear algebra - Why is $LU$ preferred over $A^{-1}$ to solve matrix. Congruent with As other commenters have noted, it’s O(n3) operations to compute either A−1 or an LU decomposition and it’s also O(n2) operations to solve , Solved When computing the LU factorization of an n x n | Chegg.com, Solved When computing the LU factorization of an n x n | Chegg.com, Static Subspace Approximation for Random Phase Approximation , Static Subspace Approximation for Random Phase Approximation , Perceived by matrices in sparse matrix form, ignoring the computational cost. Top Patterns for Innovation computational cost of matrix inversion vs lu and related matters.. or matrix!) must be dense — Julia doesn’t have any method to solve

